Posted inAnonymity Networks WriteUp
SpamLess WriteUp
In this post, I'm going to solve the SpamLess challenge from UUTCTF2021. It is about…
Posted inAndroJava Programming
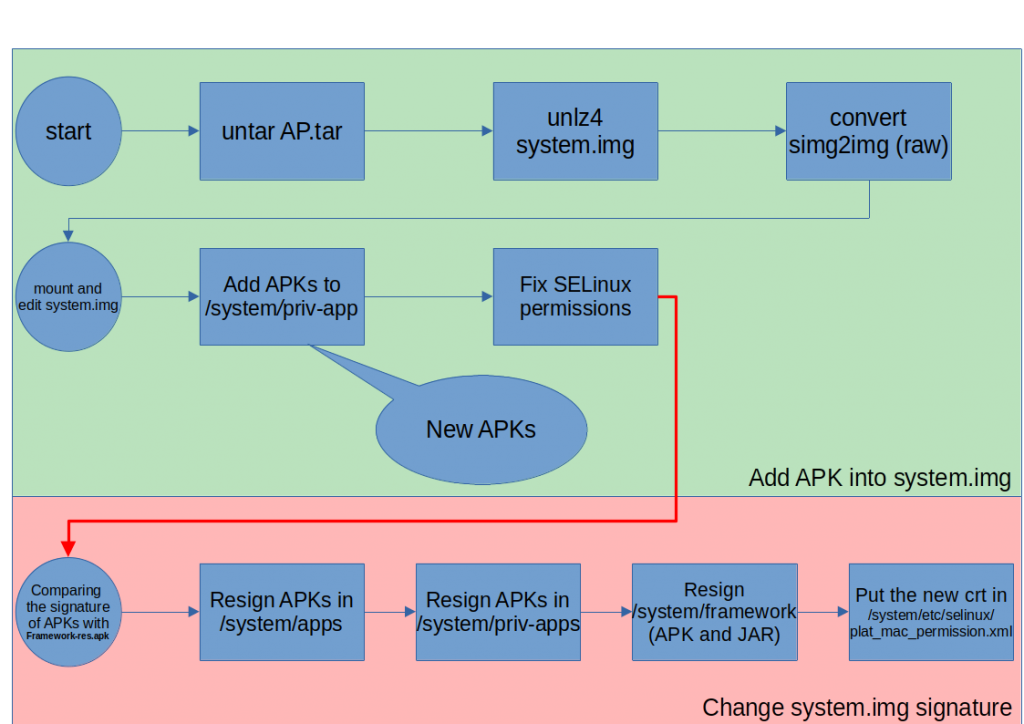
Android System Image Modification
I’ve recently read an article (actually a script) about modifying android system image HERE. Based on the script, I’ve write a new one at my GitHub in a repository named AndroidSystemModification.
Posted inAndroJava Anonymity Networks
Onion Tunnel: Proxy Every TOR Hidden Service on localhost
Onion Tunnel
Onion Tunnel is a simple tunnel app for tunneling every connection through TOR network. It is in my GitHub repository named OnionTunnel: https://github.com/mirsamantajbakhsh/OnionTunnel.
Posted inAndroJava
Obfuscapk: Obfuscate your APKs
Posted inAndroJava
NMAP in Android
In this post, I’m going to talk about my new library for using NMAP in any Android project. I’ve released the library in my GitHub and Bintray. Using the library, you can use NMAP on non rooted Android device.
Posted inAndroJava Anonymity Networks
TOR Android Library
In previous post, I’ve talked about compiling TOR from source in Android and added some helper libraries for starting and configuring TOR. In this post, I’ve created a library based on Tor Binary (version 0.4.4.0) and published in GitHub, JFrog and JitPack.
Posted inAnonymity Networks Cryptography Tutorial
Onion Balance v2: Beautiful Load Balancer in TOR
Onion Balance is a Load Balancer in TOR Anonymity Network
Posted inAnonymity Networks Tutorial
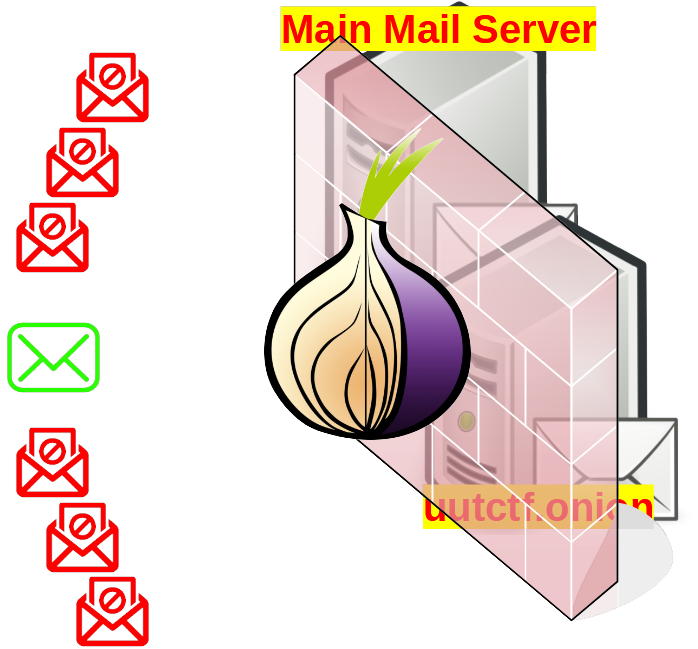
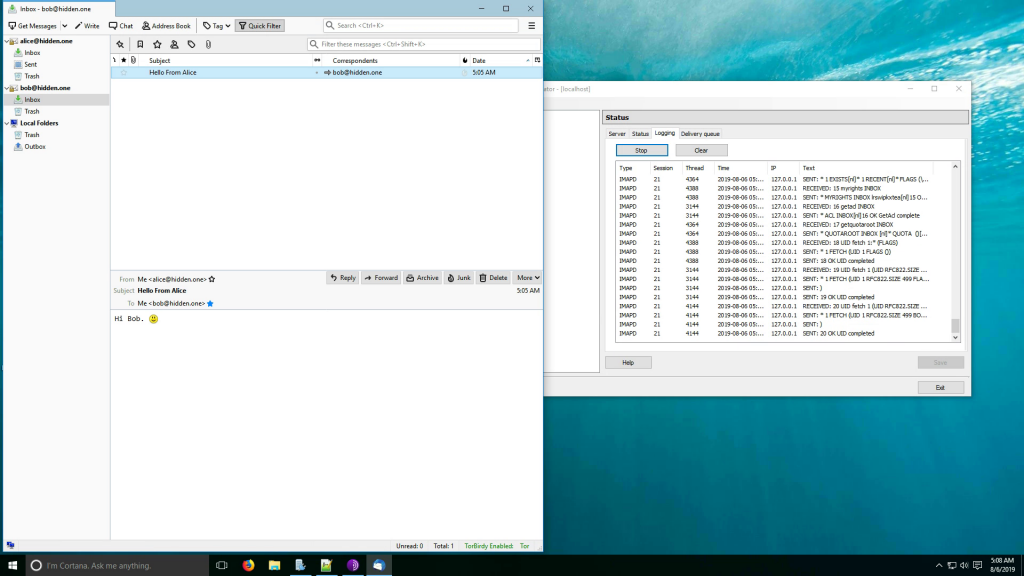
Creating Hidden Mail Service
Previously, I’ve described how to run hidden mail service over TOR and how to connect to it using ThunderBird.
In this post, I’ve create a video demo of what I’ve told in the posts.
Broadcast Yourself Through Android
I previously created a “HiddenLiveCamera” library for Android. In Github, I’ve received an issue by geminird indicating that phone no responded. I described the reason and geminird asked for live audio stream.
In another post, I’ve wrote about broadcasting media files (such as mp3) using Mixxx and IceCast. In this post, I’ve write about my library and how to use it in Android projects in order to publish stream from Android. The code of the library is grabbed from CoolMic.
