Onion hMailServer
Posted inAnonymity Networks Cryptography Tutorial

Configuring a Hidden Email Server

January 17, 2019

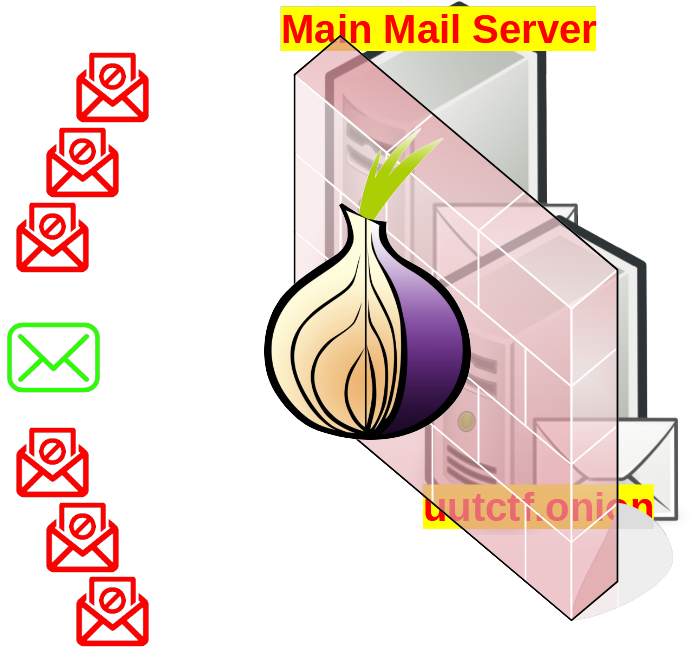
In this post, I will talk about configuring an Email server which is accessible using TOR. Using TOR will make its IP to be hidden, also accessible if it is behind NAT (inside a home computer without a public IP). But the main question is why one should use this kind of scenario?

Many people may not trust messaging services such as Telegram or WhatsApp but want to have their own private communication system. In this tutorial, you can run your own mail server in your home LAN and access it through Internet without spending money for public IP or VPS.

For the email server part, I will use hMailServer, an open source email server developed for windows.

IlamCTF
Posted inAndroJava WriteUp

Ilam CTF: Android Reverse WriteUp

November 24, 2018

Ilam CTF has been hold on 23rd Nov 2018. Unfortunately I’ve planned other things for 22-23 Nov 2018 and because of the delay in holding the CTF, I couldn’t attend this CTF.

However, I could download the Android Reverse question for future analysis. And the flag is here:

ilam_ctf_0a095194dbcf4f798751aaafdfb_1db6b2ed339f4698b6b38b5e7ae

But the WriteUP!