Latent Dirichlet Allocation

What is Latent Dirichlet Allocation?

In a general view, LDA is an unsupervised method for clustering documents. It models (purified) documents as bag of words. Also it assumes each word (and document) has a mixture model of topics i.e. each word (and document) may belongs to each of the topics by a probability. It takes number of clusters in the corpus as input then, simply assigns each word in each document a random topic. Then tries for

It was a very general description of LDA.

How it is work?

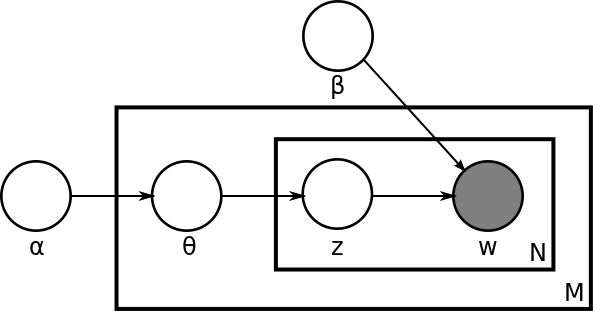
The process of LDA depends on the bag of words model of documents. First of all there are K topics that is input of LDA (guessed!). We have totally D documents and V distinct vocabulary in the document set. The generative process is:

1. For k = 1 … K:
   1. φ(k) ∼ Dirichlet(β)
2. For each d in D:
   1. Θ_d ∼ Dirichlet(α)
   2. For each word w_i in d
      1. z_i ∼ Discrete(θ_d)
      2. w_i ∼ Disctete(φ^(z_i⁾)

This is the total process. But what it means?

Dirichlet

In simple words, Dirichlet is a probabilistic distribution that has K concentration parameters. Each parameter (α) is a random number greater than zero (α > 0). Following is an example of Dirichlet distribution for 20 documents with 4 topics. Parameters for this example (α₁ = 10, α₂ = 5, α₃ = 3, and α₄ = 20).

φ(k)

This is a Dirichlet distribution for the K^th topic. The φ is a KxV matrix where each element is the probability of belonging the v^th word to the k^th topic.

Θ_d

Similarly the Θ_d is a Dirichlet for the document d. It shows the belonging of the document to each of the topics.

Finally

The process is as below in simple words:

1. For each topic:
   1. Randomly initialize belonging probability of each word in vocabulary to the topics.
2. For each document:
   1. Randomly initialize belonging probability of current document to the topics.
   2. For each word:
      1. Choose a topic from Θ_d (z_i)
      2. Randomly choose a new word from φ(k) where k is the selected topic in the previous part.

The last step, helps us to find words similar to the current chosen one to be in same cluster.

In the next post, I will explore the mathematics behind the LDA. Any comments?