In the previous post (Latent Dirichlet Allocation),  I’ve described the LDA process and how it can be applied on documents.

In this post I will explain how the probabilities can be estimated using collapsed Gibbs sampling.

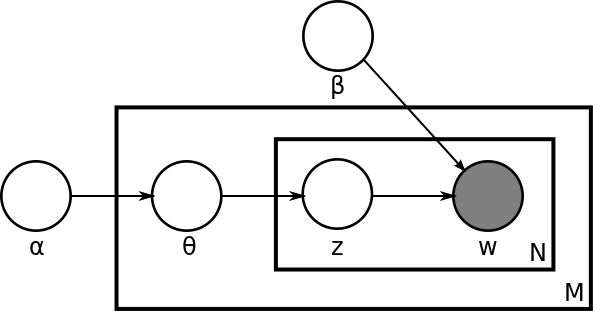
Lets start with the LDA Probabilistic Graph Model.

Where W is the sampled word from document, Z is the topic assigned by Document (d), θ is the Dirichlet distribution of d, α and β are the input of Dirichlets. More info about hyperparameters can be found this link.

So the only known variables are α, β, and w. All others (z, θ, and φ) are unknown. So based on the LDA graph we have:

p(w, z, θ, φ | α, β) = p(φ|β) p(θ|α) p(z|θ) p(w|φ_z)

The right side of the above conditional probability can be reached by the probabilistic graph model where each variable only depends on its parent nodes.